布莱克-休斯-墨顿模型(Black-Scholes-Merton model)是最重要的现代投资学理论成果之一,不仅是投资银行(investment bank)和避险基金(hedge fund)对选择权(option)合约进行定价的理论基础,还对整个衍生品市场的定价产生了深远影响。
布莱克-休斯-墨顿模型(Black-Scholes-Merton model)的创造者1968年,经济学家Fisher Black和Myron Scholes证明了风险中性论(risk neutral argument),他们的想法基於市场研究人员和从业人员以前所做的工作。随後他们尝试将公式应用於市场,但由於再交易中缺乏风险管理,造成了经济损失。
1973年,经过进一步的努力,布莱克和休斯在《政治经济杂志》上发表了名为“选择权和公司负债的定价”的论文。同年晚些时候,Robert C Merton在《贝尔经济学与管理科学杂志》上发表了名为“理性选择权定价理论”的论文。墨顿改进了布莱克-休斯模型,使其不依赖於资本资产定价模型(Capital Asset Pricing Model),并将股息纳入选择权模型中。
1997年,由於对衍生品定价的贡献,休斯和墨顿获得了诺贝尔经济学奖(由於布莱克不幸於1995年逝世,因此没能获奖,但其贡献得到了诺贝尔奖委员会的肯定)。
布莱克-休斯模型(Black-Scholes model)的基本假设金融市场假设:
金融资产假设:
关於衍生品市场的无风险利率,请参考《简谈关於利率的几个最基本的问题:国债收益率曲线、OIS零息利率曲线》
金融市场的第1条假设显然成立;第2、3条假设是合理的,因为衍生品市场的主要参与者是大型机构投资者,他们有充足的资金可以参与任意市场的交易;第4、5条假设对模型的影响不大,因为大型机构投资者的交易成本较低,并且计算机技术的发展使得套利变得很难。
金融资产的第1、4条假设对模型的影响不大,可以将变化的无风险利率和股息纳入模型;第2、3条假设是基於资本资产定价模型(Capital Asset Pricing Model);第5条假设是为了研究方便,可以将美式选择权纳入模型。
无中间收入资产的布莱克-休斯-墨顿(Black-Scholes-Merton)定价公式无中间收入资产的布莱克-休斯-墨顿定价公式如下:
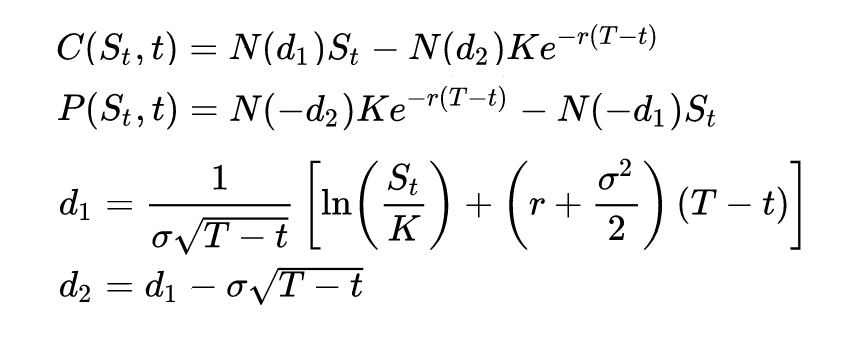
其中:
C(St,t)和P(St,t)分别是执行价格为K、到期日为T的欧式买权和欧式卖权在时间t的理论价格;
N(d1)和N(d2)分别是d1和d2的常态分布的累积分布函数值;
St是无股息股票(标的资产)在时间t的价格;
σ是无股息股票(标的资产)期望报酬率的波动率;
r是连续形式的无风险利率。
如何理解公式?简言之,该模型“相当於”微积分版本的二项选择权定价模型(Binomial Options Pricing Model)。
投资银行和避险基金在设计选择权合约时,可以参考上述公式,这意味著,只需知道标的资产的价格S、执行价格K、到期日T、标的资产期望报酬率的波动率σ和无风险利率r,就可以计算出欧式选择权在时间t的理论价格。
除了标的资产期望报酬率的波动率σ,其他数据都可以从市场获得。交易所提供给投资者的是基於选择权价格计算出的隐含波动率(Implied Volatility)。隐含波动率反映了选择权市场对未来标的资产价格的预期。与之相关的是历史波动率,历史波动率是基於过去数据计算出的数据,不包含对未来的预期。
有中间收入资产转化为无中间收入资产的布莱克-休斯-墨顿(Black-Scholes-Merton)定价公式上文公式是无股息股票(不产生中间收入的标的资产)的选择权定价的参考标准,如何将股息股票(或其他产生中间收入的标的资产,如长期持有外汇多头)纳入模型中呢?
根据无套利均衡(no arbitrage equilibrium)原理,产生中间收入的资产的当前价格反映了两部分价值,一部分是中间收入的价值,另一部分是转卖资产可获得的价值(资本报酬);不产生中间收入的资产的当前价格只反映了转卖资产可获得的那部分价值。因此,理论上将所有中间收入的贴现值从产生中间收入的标的资产价格中剥离出去,就得到不产生中间收入的标的资产价格。
具体而言,带股息股票价格减去预期股息贴现值,就转化成无股息股票;(St→St×exp(-q(T-t)),q为连续形式的预期股息率)
外汇的美元价格(如EUR/USD汇率、GBP/USD汇率)减去外汇利息贴现值,就转化为无息外汇。(St→St×exp(-rf(T-t)),rf为连续形式的外汇利率)
除了预期股息,其他数据都可以从市场获得。对股息的估计值可以根据历史股息,也可以根据公司财报。
因此,分别用St×exp(-q(T-t)),St×exp(-rf(T-t))代替上文公式中的St,就得到股息股票、外汇的选择权定价 健�
标的资产为期货的选择权定价公式显然,有中间收入资产的选择权定价公式使用不便,还可以进一步简化为相应标的资产期货的选择权定价公式。理论上可以证明,和选择权同时到期的期货上的选择权等价於原标的资产的选择权。此外,提供标的资产为交易所旗下的期货合约的选择权合约非常方便,例如CME集团提供的选择权合约都是以该集团旗下的期货合约为标的资产。
根据无套利均衡的远期定价,可以用Ft×exp(-r(T-t))分别代替St×exp(-q(T-t)),St×exp(-rf(T-t)),就得到更加方便的期货选择权定价公式。(理论上,远期价格略小於期货价格,二者的差异对模型的影响不大)
股票期货选择权定价公式
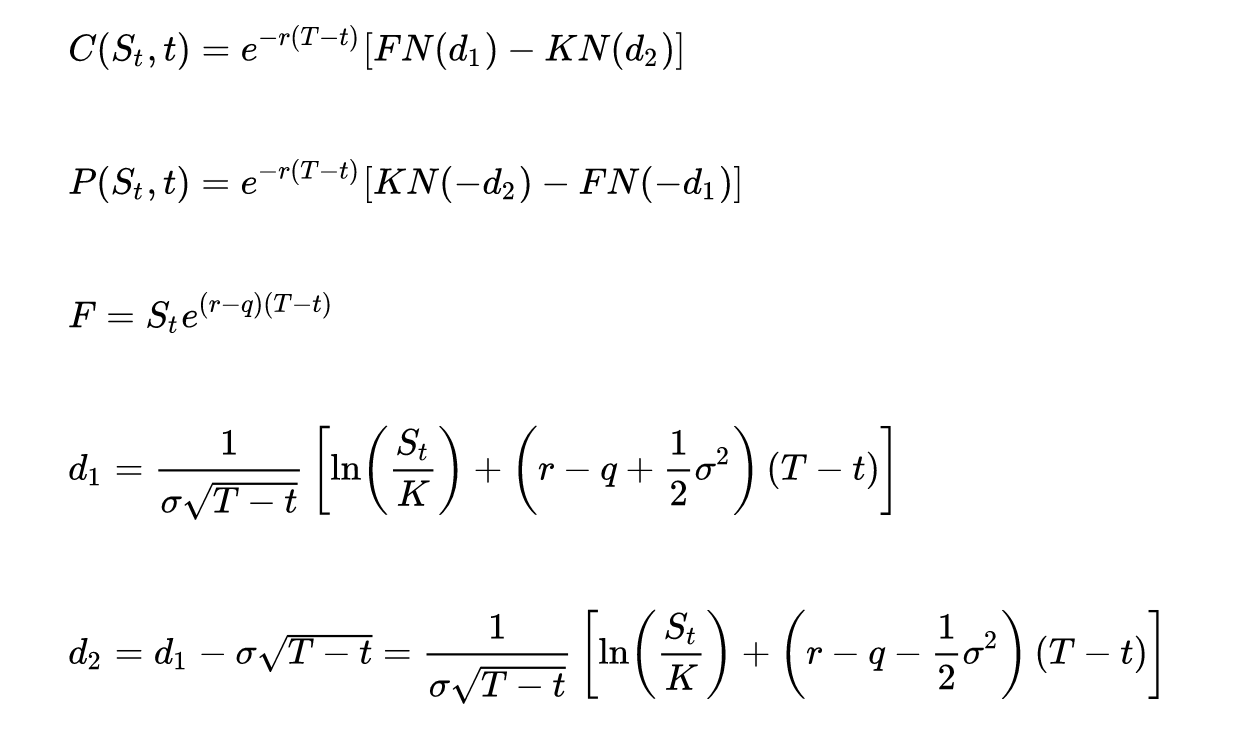
F为股票期货在时间t的价格,q为连续形式的预期股息率。值得注意的是,将第三行期货定价公式代入第四、五行後将消去q,d1和d2将不含q,对外汇期货也有类似的结论。
上述公式对无中间收入资产和有中间收入资产的选择权均适用,并且不需要考虑有中间收入资产的q/利息率/rf。
这意味著,只需知道标的资产期货价格F、执行价格K、到期日T、标的资产期货的期望报酬率的波动率σ(可以证明,标的资产和标的资产期货的期望报酬率的波动率相等)和无风险利率r,就可以计算出欧式选择权在时间t的理论价格。
买卖权平价关系与选择权上下限上述用期货价格代替标的资产价格的方法也可以应用到买卖权平价关系式中,并应用无套利假设得到选择权价格的上下限:
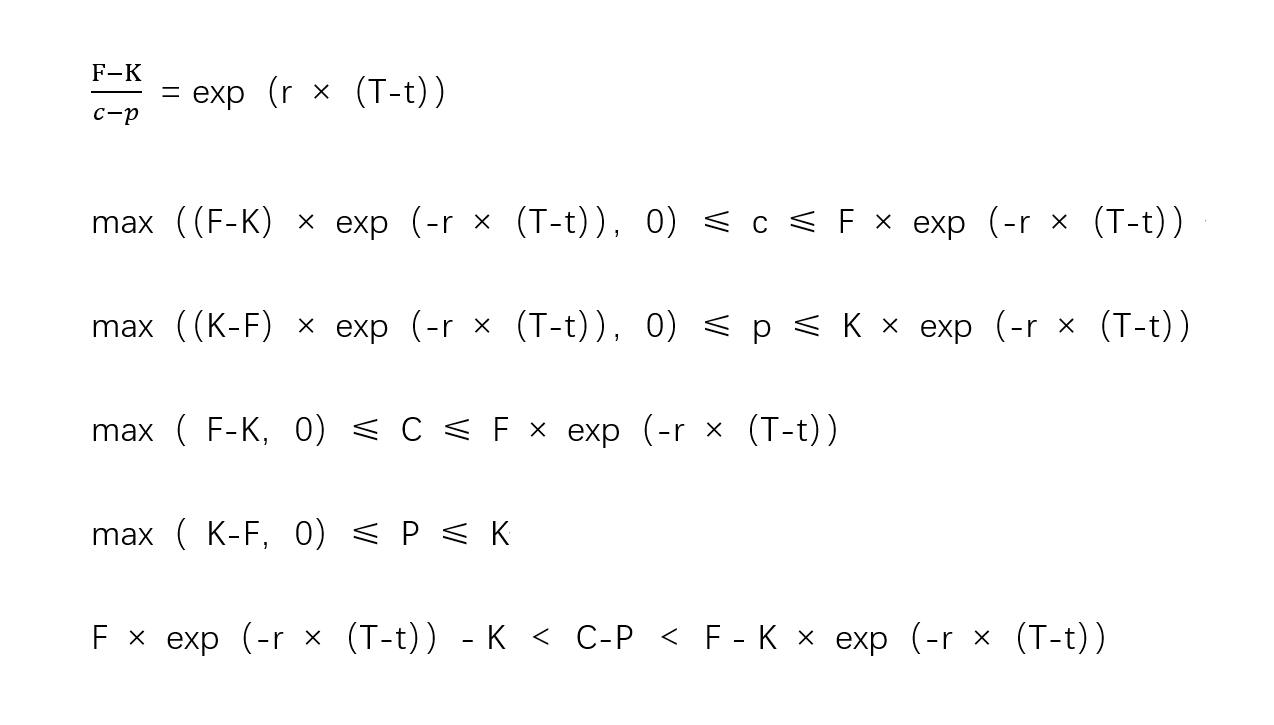
c、p、C、P分别为欧式买权、欧式卖权、美式买权、美式卖权的价格。上述关系式可以检验市场是否存在套利机会。
隐含波动率并非常数对选择权市场的实证研究表明,隐含波动率并非常数。隐含波动率σ与执行价格K的关系成为波动率曲线(volatility curve),隐含波动率与执行价格K、选择权期限T的关系称为波动率曲面(volatility surface)。
对股票选择权来说,波动率曲线可能呈波动率倾斜(volatility skew)形态,即较低执行价格的隐含波动率高於较高执行价格的隐含波动率(例如,SPX与VIX反相关)。
股票波动率曲线也可能呈波动率皱眉(volatility frown)形态,例如股票基本面面临不确定性事件时,选择权市场可能表现为,当前股价附近的波动率上升,而偏离当前价格的波动率下降。
对外汇选择权来说,波动率曲线可能呈波动率微笑(volatility smile)形态,即价平(at the money)选择权的隐含波动率低於价内(in the money)和价外(out of the money)选择权的隐含波动率。
为什么波动率不是常数?一种解释是布莱克-休斯-墨顿模型关於金融资产的基本假设3是股票价格服从对数常态分布,也就是假设波动率为常数。事实上,波动率并非常数。
对波动率倾斜的一种解释是,股票市场认为价格下跌的可能性大於上涨的可能性,这会增加较低执行价格的选择权的隐含波动率。
对波动率微笑的一种解释是,汇率的实际分布可能比对数常态分布具有更“肥尾”的特征,换言之,外汇市场认为汇率出现极端值的可能性大於布莱克-休斯-墨顿模型认为的可能性。
这并不是说布莱克-休斯-墨顿模型是错误的,该模型仍然是投资从业人员最重要的理论参考之一。
从这里去往何处布莱克-休斯-墨顿模型为投资从业人员提供了选择权价格的理论基础,并且提供了衍生品定价的一般思路。该模型找到了决定选择选择权的价格的因素——标的资产(期货)价格、执行价格、时间(期限)、无风险利率、标的资产(期货)价格期望报酬率的波动率(隐含波动率)。我们将从这里出发,分析这些因素对选择权价格的影响(选择权的希腊字母)。
你可能还想知道这些选择权/期权(option)交易策略:
《期权(选择权)基础策略(一):保护(cover)》
《期权(选择权)基础策略(二)∶看涨价差、看跌价差(bull & bear spread)》
《期权(选择权)基础策略(三):蝴蝶价差(butterfly spread)》
《期权(选择权)基础策略(四):跨式(straddle)、宽跨式(strangle)》
笔者向想要系统地学习期权(选择权)的读者建议Tastylive中文内容研究员曾凯老师的《期权(选择权)面面观》视频系列,笔者从中获益匪浅。